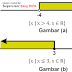
- Tentukan himpunan penyelesaian pertidaksamaan berikut, kemudian gambarkan dalam garis bilangan.(a) 2x + 8 > 0 (b) 5x – 15 ≤ 0 Jawab: (a) 2x + 8 > 0⇒ 2x > −8⇒ x > −4Jadi, himpunan penyelesaiannya adalah {x | x > −4, x ∈ R}. Himpunan penyelesaian ini, secara geometris tampak pada Gambar (a).(b) 5x – 15 ≤ 0

⇒ 5x ≤ 15
⇒ x ≤ 3
Jadi, himpunan penyelesaiannya adalah {x | x ≤ 3, x ∈ R}. Garis bilangannya dapat digambarkan seperti pada Gambar (b).
2. Carilah himpunan penyelesaian pertidaksamaan berikut ini.
(a) 2 – 3x ≥ 2x + 12
(b) 4x + 1 < x – 8
Jawab:
(a) 2 – 3x ≥ 2x + 12
⇒ −2x – 3x ≥ −2 + 12
⇒ −5x ≥ 10
⇒ x ≤ −2
Jadi, himpunan penyelesaian pertidaksamaan itu adalah {x | x ≤ −2, x ∈ R}.
(b) 4x + 1 < x – 8
⇒ 4x – x < −8 – 1
⇒ 3x < −9
⇒ x < −3
Jadi, himpunan penyelesaian pertidaksamaan itu adalah {x | x < −3, x ∈ R}.
3. Carilah himpunan penyelesaian dari setiap pertidaksamaan linear berikut ini.
(a) 2x – 1 < 0
(b) 3x – 6 > 0
Jawab:
(a) 2x – 1 < 0
⇒ 2x < 1
⇒ x < 1/2
Jadi, himpunan penyelesaiannya, HP = {x | x < 1/2}.
(b) 3x – 6 > 0
⇒ 3x > 6
⇒ x > 6/3
⇒ x > 2
Jadi, himpunan penyelesaiannya, HP = {x | x > 2}.
4. Nilai x yang memenuhi pertidaksamaan ,x∊R adalah...
,x∊R adalah...
a. 1 < x < 2
b. 5 < x < 25
c. x < -1 atau x > 2
d. x < 1 atau x > 2
e. x < 5 atau x > 25
Pembahasan:
(p – 25) (p – 5) = 0
p = 25 dan p = 5
Untuk p = 25, maka nilai x:
x = 2
Untuk p = 5, maka nilai x:
x = 1
HP = {1 < x < 2}
Jawaban: A